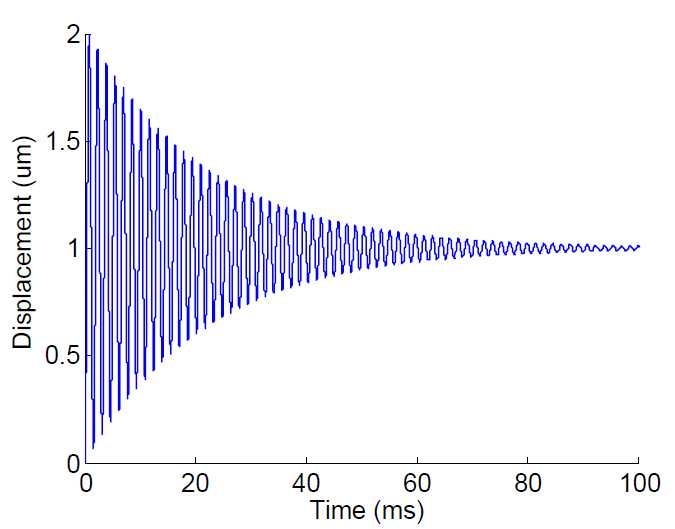
系统零点与震荡里面提到过反馈系统里面抵消震荡的原理,我这次想聊一下前馈法,英文里面一般叫feedforward compensator,也有叫input shaper的,也有搞信号的就叫它是一个filter,anyway。前馈法的优点是什么?便宜,不用买传感器;不会带来稳定性问题。
如果对于一个线性度很好的稳定的震荡系统,前馈法抵消应该是个很容易的事情:引入一对前馈的零点(notch filter),把震荡的极点对给抵消了不就好了么。问题是,这个零点对怎么实现?纯微分都不好实现,那一对共轭的零点麻烦就会更大。其实有个经典的前馈控制器叫做posicast controller:
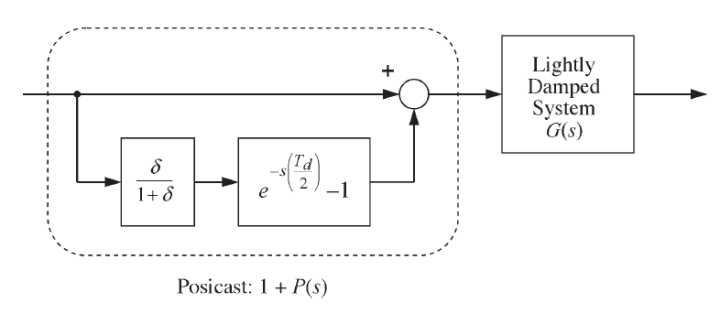
它的控制框图也很简单:
图片来自文献[1]。
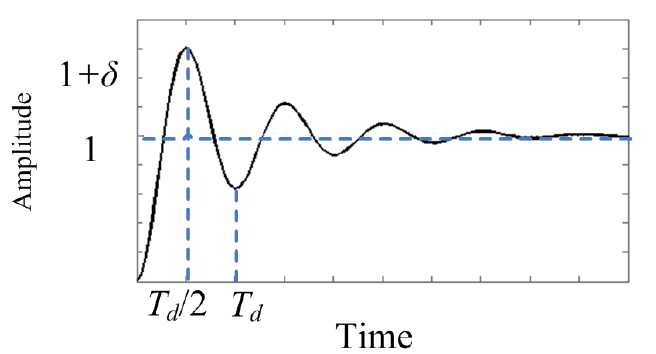
其中的δ和Td是非常直观的,对于工程师们是非常容易理解和实现的,如下图的例子,前者是超调量,后者是超调时间:
在根轨迹上来看一下发生了什么:
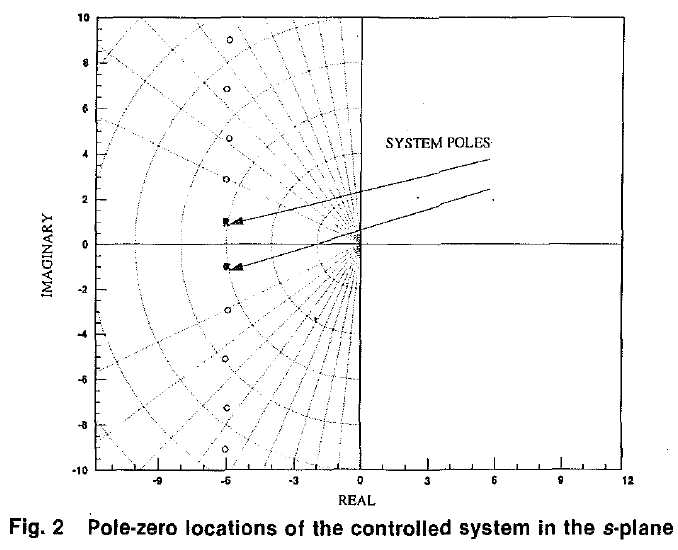
图片来自文献2,我就不手绘了。公式(1)其实是有个无穷零点的系统,而它的第一对零点就用来抵消掉那个不希望有的震荡极点对。它比notch好的地方在于,它的高频增益是很低的,而不像notch那样过了陷波之后就会一路走高,看它自己的不加log scale频域图的一个例子:
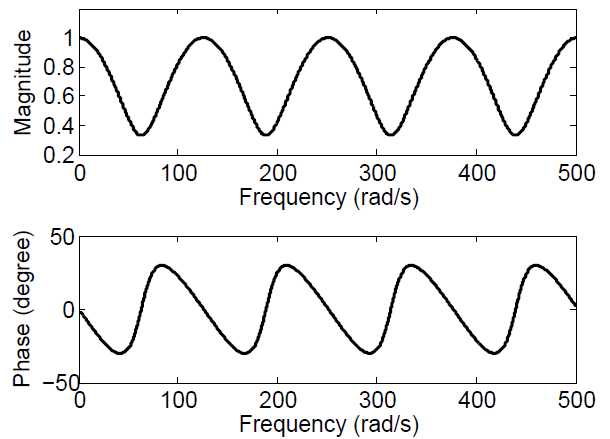
可见它的幅值增益是不会超过1的。即对于高频的前馈噪声不敏感。再看一个在频域下抵消了震荡极点之后的图:
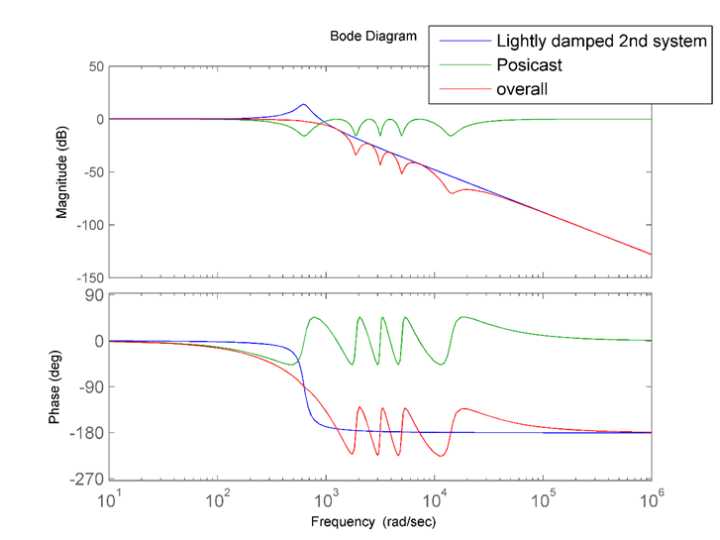
看红线明显可得知震荡极点对被抵消了。
这个方法对于线性度好的稳定系统相当有效,但是如果这个极点对和零点对不匹配呢?答案是鲁棒性比较差,即使有着比较小的不匹配,效果也会大打折扣:
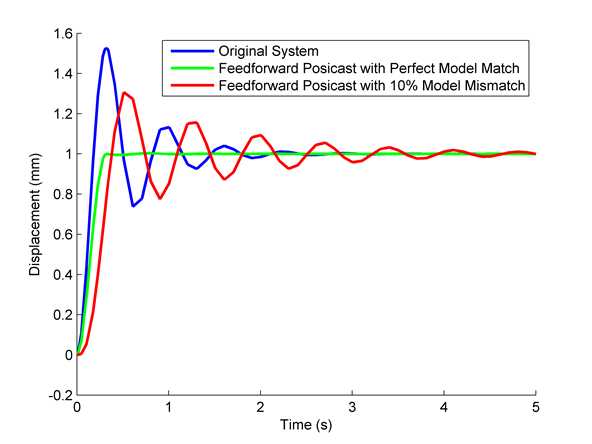
前馈法是否就山穷水尽了?并不是。下一次我会给大家介绍一下robustness更好一些的前馈控制器。
前馈形式的震荡控制器(下)
[1] Hung, John Y. "Feedback control with Posicast." IEEE Transactions on industrial electronics 50.1 (2003): 94-99.
[2] Singh, Tarunraj, and S. R. Vadali. "Robust time-delay control." Journal of dynamic systems, measurement, and control 115.2A (1993): 303-306
本文转载自知乎,作者:李崇,如若转载请联系原作者。